Bayes in Wonderland! Predictive supervised classification inference hits unpredictability

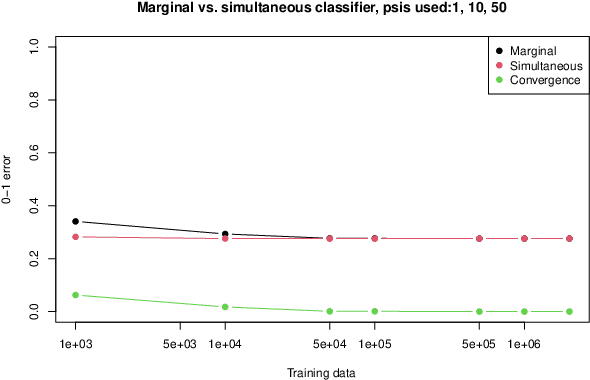
The marginal Bayesian predictive classifiers (mBpc) as opposed to the simultaneous Bayesian predictive classifiers (sBpc), handle each data separately and hence tacitly assumes the independence of the observations. However, due to saturation in learning of generative model parameters, the adverse effect of this false assumption on the accuracy of mBpc tends to wear out in face of increasing amount of training data; guaranteeing the convergence of these two classifiers under de Finetti type of exchangeability. This result however, is far from trivial for the sequences generated under Partition exchangeability (PE), where even umpteen amount of training data is not ruling out the possibility of an unobserved outcome (Wonderland!). We provide a computational scheme that allows the generation of the sequences under PE. Based on that, with controlled increase of the training data, we show the convergence of the sBpc and mBpc. This underlies the use of simpler yet computationally more efficient marginal classifiers instead of simultaneous. We also provide a parameter estimation of the generative model giving rise to the partition exchangeable sequence as well as a testing paradigm for the equality of this parameter across different samples. The package for Bayesian predictive supervised classifications, parameter estimation and hypothesis testing of the Ewens Sampling formula generative model is deposited on CRAN as PEkit package and free available from https://github.com/AmiryousefiLab/PEkit.

Inductive Inference in Supervised Classification

Inductive inference in supervised classification context constitutes to methods and approaches to assign some objects or items into different predefined classes using a formal rule that is derived from training data and possibly some additional auxiliary information. The optimality of such an assignment varies under different conditions due to intrinsic attributes of the objects being considered for such a task. One of these cases is when all the objects' features are discrete variables with a priori known categories. As another example, one can consider a modification of this case with a priori unknown categories. These two cases are the main focus of this thesis and based on Bayesian inductive theories, de Finetti type exchangeability is a suitable assumption that facilitates the derivation of classifiers in the former scenario. On the contrary, this type of exchangeability is not applicable in the latter case, instead, it is possible to utilise the partition exchangeability due to John Kingman. These two types of exchangeabilities are discussed and furthermore here I investigate inductive supervised classifiers based on both types of exchangeabilities. I further demonstrate that the classifiers based on de Finetti type exchangeability can optimally handle test items independently of each other in the presence of infinite amounts of training data while on the other hand, classifiers based on partition exchangeability still continue to benefit from joint labelling of all the test items. Additionally, it is shown that the inductive learning process for the simultaneous classifier saturates when the amount of test data tends to infinity.

Asymptotic Supervised Predictive Classifiers under Partition Exchangeability

The convergence of simultaneous and marginal predictive classifiers under partition exchangeability in supervised classification is obtained. The result shows the asymptotic convergence of these classifiers under infinite amount of training or test data, such that after observing umpteen amount of data, the differences between these classifiers would be negligible. This is an important result from the practical perspective as under the presence of sufficiently large amount of data, one can replace the simpler marginal classifier with computationally more expensive simultaneous one.